The counting Principle: If two jobs need to be completed and there are M ways to do the first job & N ways to do the second Job, then there are M*N ways to do one job followed by the other, This principle may be extended to any number of jobs.
Example: Alina has 4 paintings in her bedroom. She is going to bring up 2 of them and hang 1 in the drawing room & 1 in the dining room. In how many ways can she choose which painting go in each room?
Solution: Here the first job is to pick one of the 4 paintings and hang it in the drawing room. The second job was to choose one from among the remaining 3 & hang it in the dining room. So, there are 3x4 =12 ways of doing this.
Venn Diagram: A Venn diagram is a drawing in which circular areas represent groups of items sharing common properties. The drawing consists of two or more circles, each representing a specific group i.e. a number of items sharing some particular properties. This process of visualizing logical relationships was devised by John Venn.

Each Venn diagram starts with a rectangle representing the universal set i.e. the set of all the objects in the problem. Then each set in the problem is represented by a circle in the rectangle. Any value that belongs to more than one set is placed in the area where the circles overlap.
Let us illustrate the concept with an example: A schools has 100 seniors. The following Venn diagram shows the distribution of these students in the band & the orchestra. Here the universal set has 100 students. The 32 written in the part of the diagram where the two circles overlap represents these seniors who belong to both the orchestra and the band. 37 seniors are in the orchestra but not in the band. Similarly, 18 seniors are in the band but not in the orchestra. Last of all, the 13 written outside the circles, represent those seniors who are neither in the orchestra nor the band.
We can now make a cross check. All the different sets should add up to give the universal set.
37+32+18+13=100=> The universal set
One important thing to notice is that, the orchestra has 37+32 = 69 seniors & the band has 32+18=50 seniors. Be careful that seniors in orchestra + seniors in band + seniors in none = 69 + 50 + 12 + 132 =>100
Here we have counted the seniors who are in both orchestra & band twice. So, when you are asked to find the total, always be careful to include the common cases only once.
Some Important Venn Diagram Formula With Question:
The problems are seemingly the same. Let’s now look at this problem from the perspective of a venn diagram.
 If we want to know the probability that event A or event B occurs, we clearly can see that we have:
If we want to know the probability that event A or event B occurs, we clearly can see that we have:
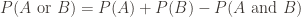
(We have to subtract that last term, because we added that overlapping section twice when we took .)
.)
Let’s apply that to our two questions:
Question 1: We have a probability of: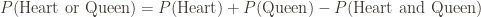 . Clearly
. Clearly 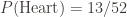 and
and 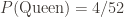 . What is
. What is  ? Intuitively — or using our venn diagram — we know it is 1/52. And the answer works out correctly to 16/52.
? Intuitively — or using our venn diagram — we know it is 1/52. And the answer works out correctly to 16/52.
Question 2: We have a probability of: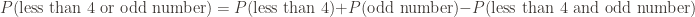 . Clearly
. Clearly 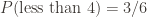 and
and 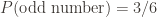 . What is
. What is  ? Intuitively — or using our venn diagrams — we know it is 2/6. And the answer works out correctly to 4/6.
? Intuitively — or using our venn diagrams — we know it is 2/6. And the answer works out correctly to 4/6.
However, let’s say we wanted to calculate and
and  (the overlapping regions) mathematically? It turns out that there is something fundamental that makes these two problems different. In
question 1, the two events (drawing a heart / drawing a queen) are
independent. In question 2, the two events (rolling a number less than 4
/ rolling an odd number) are dependent. For the first question, you can
say that
(the overlapping regions) mathematically? It turns out that there is something fundamental that makes these two problems different. In
question 1, the two events (drawing a heart / drawing a queen) are
independent. In question 2, the two events (rolling a number less than 4
/ rolling an odd number) are dependent. For the first question, you can
say that  while in the second problem you cannot do that.
while in the second problem you cannot do that.
Recall that the definition of independence of two events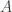 and
and 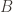 is if
is if 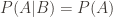 .
.
Checking the first question for independence, we see that the probability of drawing a heart given that you already have a queen is 1/4, and that is the same as the probability of drawing a heart (1/4). (Similarly, the probability of drawing a queen given that you already have a heart is 1/13, and that is the same as the probability of drawing a queen (1/13).) So the two events are independent.
Checking the second question for independence, we see that the probability of rolling and odd number given that you have rolled a number less than 4 is 2/3, while the probability of rolling an odd number is 1/2. (Similarly, the probability of rolling a number less than 4 given that you’ve rolled an odd number is 2/3, while the probability of rolling a number less than 4 is 1/2.) So the two events are dependent.
The teacher who brought up this problem was grading exams, and one student had calculated . And seeing the two problems were almost identical, calculated
. And seeing the two problems were almost identical, calculated 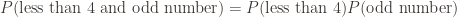 — which, as we know, isn’t right for dependent events.
— which, as we know, isn’t right for dependent events.
What we were discussing is how we could explain to the student that the two situations are different, even though on the surface the questions seem like they are of the same form. In other words, is there a conceptual — non mathematical — way to explain that the first question involves independent events while the second question involves dependent events? It certainly isn’t intuitive, at least not to me.
Download: Sets, Venn Diagrams & Counting - Arizona State University
Venn diagram
Example: Alina has 4 paintings in her bedroom. She is going to bring up 2 of them and hang 1 in the drawing room & 1 in the dining room. In how many ways can she choose which painting go in each room?
Solution: Here the first job is to pick one of the 4 paintings and hang it in the drawing room. The second job was to choose one from among the remaining 3 & hang it in the dining room. So, there are 3x4 =12 ways of doing this.
Venn Diagram: A Venn diagram is a drawing in which circular areas represent groups of items sharing common properties. The drawing consists of two or more circles, each representing a specific group i.e. a number of items sharing some particular properties. This process of visualizing logical relationships was devised by John Venn.

Each Venn diagram starts with a rectangle representing the universal set i.e. the set of all the objects in the problem. Then each set in the problem is represented by a circle in the rectangle. Any value that belongs to more than one set is placed in the area where the circles overlap.
Let us illustrate the concept with an example: A schools has 100 seniors. The following Venn diagram shows the distribution of these students in the band & the orchestra. Here the universal set has 100 students. The 32 written in the part of the diagram where the two circles overlap represents these seniors who belong to both the orchestra and the band. 37 seniors are in the orchestra but not in the band. Similarly, 18 seniors are in the band but not in the orchestra. Last of all, the 13 written outside the circles, represent those seniors who are neither in the orchestra nor the band.
We can now make a cross check. All the different sets should add up to give the universal set.
37+32+18+13=100=> The universal set
One important thing to notice is that, the orchestra has 37+32 = 69 seniors & the band has 32+18=50 seniors. Be careful that seniors in orchestra + seniors in band + seniors in none = 69 + 50 + 12 + 132 =>100
Here we have counted the seniors who are in both orchestra & band twice. So, when you are asked to find the total, always be careful to include the common cases only once.
Some Important Venn Diagram Formula With Question:
Question 1: What is the probability that you draw a heart or a queen from a deck of cards?Both questions are simple enough. The first one is 16/52 (because there are 16 cards which are hearts or queens in a deck). The second one is 4/6 (because you can roll a 1, 2, 3, or 5).
Question 2: What is the probability that you roll a die and get a number less than 4 or an odd number?
The problems are seemingly the same. Let’s now look at this problem from the perspective of a venn diagram.
 If we want to know the probability that event A or event B occurs, we clearly can see that we have:
If we want to know the probability that event A or event B occurs, we clearly can see that we have:(We have to subtract that last term, because we added that overlapping section twice when we took
Let’s apply that to our two questions:
Question 1: We have a probability of:
Question 2: We have a probability of:
However, let’s say we wanted to calculate
Recall that the definition of independence of two events
Checking the first question for independence, we see that the probability of drawing a heart given that you already have a queen is 1/4, and that is the same as the probability of drawing a heart (1/4). (Similarly, the probability of drawing a queen given that you already have a heart is 1/13, and that is the same as the probability of drawing a queen (1/13).) So the two events are independent.
Checking the second question for independence, we see that the probability of rolling and odd number given that you have rolled a number less than 4 is 2/3, while the probability of rolling an odd number is 1/2. (Similarly, the probability of rolling a number less than 4 given that you’ve rolled an odd number is 2/3, while the probability of rolling a number less than 4 is 1/2.) So the two events are dependent.
The teacher who brought up this problem was grading exams, and one student had calculated
What we were discussing is how we could explain to the student that the two situations are different, even though on the surface the questions seem like they are of the same form. In other words, is there a conceptual — non mathematical — way to explain that the first question involves independent events while the second question involves dependent events? It certainly isn’t intuitive, at least not to me.
Download: Sets, Venn Diagrams & Counting - Arizona State University
Venn diagram
 Unknown
Unknown
 Posted in:
Posted in: 







